Физик РУДН упростил теорию Эйнштейна-Лавлока для черных дыр
Общая теория относительности Эйнштейна предсказала, что во Вселенной существуют объекты с настолько высокой плотностью, что они «притягивают» к себе даже свет — черные дыры. Существует множество математических моделей, которые описывают черные дыры, одна из них — уточнение общей теории относительности путем введения квантовых поправок, теория Эйнштейна-Лавлока. В ней черная дыра описывается с помощью суммы бесконечного числа слагаемых. Физик РУДН смог показать, что небольшого числа слагаемых достаточно, чтобы описать наблюдаемые эффекты вблизи черной дыры — остальные компоненты уравнения вносят ничтожно малый вклад, которым можно пренебречь. Это значительно упростит расчеты и поможет исследователям в изучении черных дыр в теориях с квантовыми поправками.
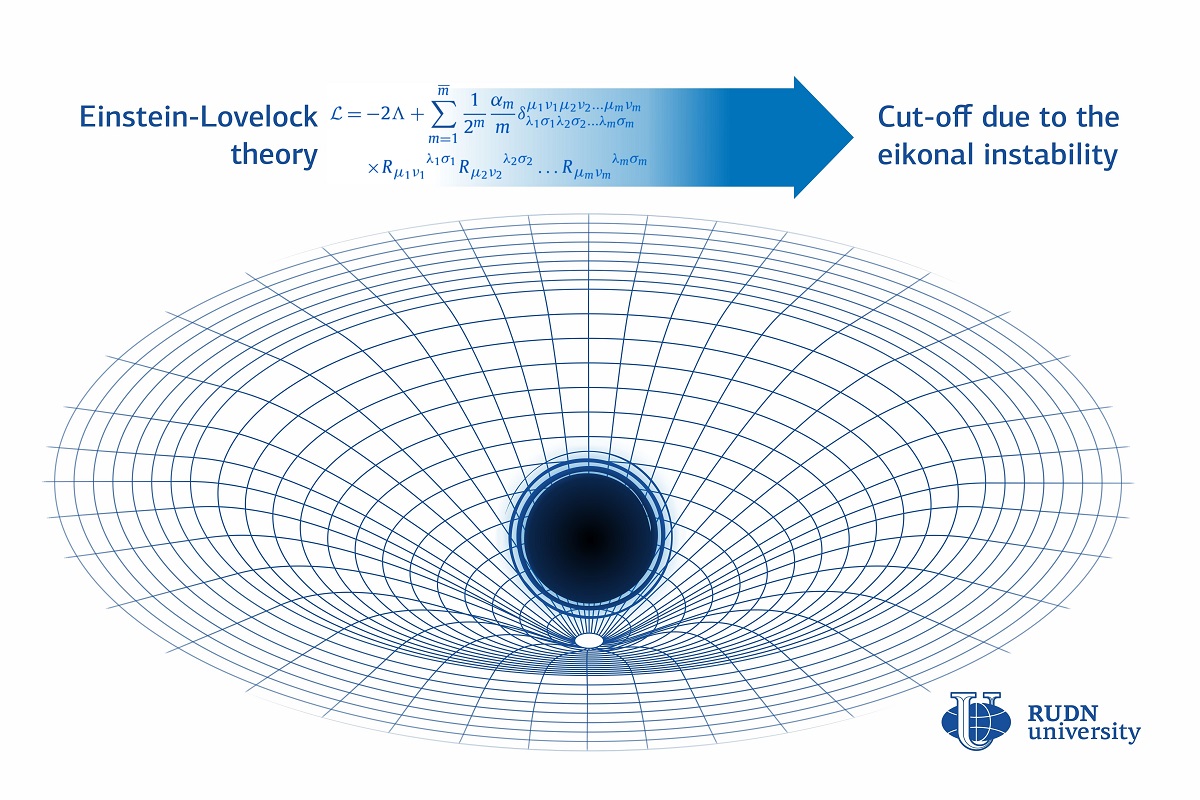
Теория Эйнштейна предполагает, что тяжелые объекты искривляют пространство-время — четырехмерную конструкции, которая включает в себя три пространственных измерения и одно временное. Лавлок в 1971 году обобщил эту теорию для любого количества измерений. Уравнение Эйнштейна-Лавлока — это бесконечная сумма: первые два слагаемых — это «обычное» эйнштейновское представление, а каждое последующее — все более детальное уточнение кривизны пространства-времени.
Каждое слагаемое в уравнении Эйнштейна-Лавлока умножается на число — так называемую константу связи. Физик РУДН показал, что, если ограничиваться положительными значениями констант связи, поправки высокой кривизны можно «отсекать». Дело в том, что для каждой константы связи можно выделить критическое значение — если константа его достигает, то черная дыра оказывается нестабильной, то есть не может существовать. Математически такое представление возможно, но физически — не имеет смысла. Чем больше слагаемых, тем меньше становится критическое значение для констант. Таким образом стабильность черной дыры — то есть возможность ее физического существования — можно использовать в качестве критерия «отсекания» ненужных слагаемых.
«С добавлением каждого слагаемого Лавлока критическое значение констант связи всегда будет уменьшаться. Это важное наблюдение, поскольку оно означает, что для оценки максимально возможной поправки к геометрии черной дыры, вызванного очередным слагаемым Лавлока, можно считать остальные слагаемые ничтожно малыми», — Роман Конопля, научный сотрудник Учебно-научного института гравитации и космологии РУДН.
Физики показали, что основные наблюдаемые величины — например, радиус тени черной дыры — практически не изменяются при включении поправок Лавлока дальше четвертого слагаемого. Эти данные будет полезны не только для изучения процессов в черных дырах, но и для проверки теоретических предсказаний связанных с возможными обобщениями теории Эйнштейна.
Работа опубликована в журнале Physics Letters B.
Сегодня диагностика и планирование лечения у ортодонтов занимает несколько дней. Также во время лечения могут возникнуть осложнения, которые замедляют процесс выздоровления пациента. Например, неправильное планирование ортодонтического лечения может привести к заболеваниям височно-нижнечелюстного сустава.
В РУДН прошла Всероссийская научно-практическая конференция с международным участием «Политические науки и наследие Великой Победы: уроки истории и современные вызовы», посвященная 80-летию победы в Великой Отечественной войне.
Монография «Судебная экспертиза: типичные ошибки», подготовленная при участии Дмитрия Сундукова, профессора, заведующего кафедрой судебной медицины медицинского института РУДН, отмечена на V конкурсе на лучшее издание, посвященное деятельности следственных органов России. Исследование получило I место в категории «Лучшее исследование криминалистического обеспечения деятельности следственных органов».